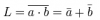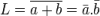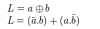Rechercher dans la communauté

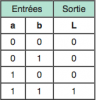
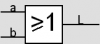
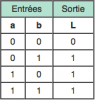
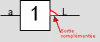
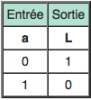
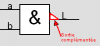
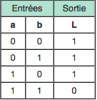
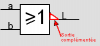
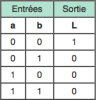
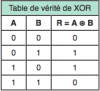
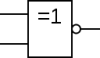
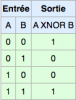
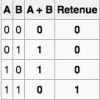
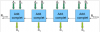
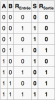
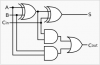
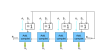
Bonjour, voici une présentation des bases de l'électronique numérique : la logique Booléenne ( ou algèbre de Boole ) . Sujet en général passionnant pour les fans d'informatique et d'électronique Tout d'abord, qu'est-ce qui ce cache derrière ce nom étrange ? : L'algèbre de Boole, ou calcul booléen, est la partie des mathématiques, de la logique et de l'électronique qui s'intéresse aux opérations et aux fonctions sur les variables logiques. Plus spécifiquement, l'algèbre booléenne permet d'utiliser des techniques algébriques pour traiter les expressions à deux valeurs du calcul des propositions. Elle fut initiée en 1854 par le mathématicien britannique George Boole. Aujourd'hui, l'algèbre de Boole trouve de nombreuses applications en informatique et dans la conception des circuits électroniques. Elle fut utilisée la première fois pour les circuits de commutation téléphoniques par Claude Shannon. Merci Wikipédia Avant de lire ce post, je vous conseille de savoir compter en binaire, si ce n'est pas votre cas, vous trouverez des explications claires ici : Bien, vous savez compter en binaire mais vous ne savez toujours pas concrètement ce qu'est l'algèbre booléenne, on avance pas décidément. L'algèbre de Boole consiste à traiter les informations avec la plus simple ( et pourtant tellemeeeeeeent complexe... ) des logique, ici l'information est soit vraie, soit fausse ( 1 ou 0 ) pas de doute possible. On va donc associer ces 0 et ces 1 grâce à ce que l'on appelle des fonctions logiques. Je vous propose donc d'étudier ces fonctions logiques de base puis de s'amuser avec pour voir leur potentiel ! I / fonctions logiques ( ou opérateurs logiques ) A/ fonction ET (conjonction) AND nous allons représenter cette fonction par un petit schéma... a et b sont nos entrées et L est la sortie de al fonction logique. Voici l'équation : L = a . b ( à lire L = a ET b ) rappelons que nous travaillons en binaire, a et b valent donc soit 0 soit 1. l'équation nous dit que L ne vaut 1 si et seulement si a ET b valent tous deux 1... d'où le nom. Un autre outil sympathique pour se représenter une fonction logique est ce que l'on appelle une table de vérité : les lignes sont à lire ainsi = "0 et 0 font 0", "0 et 1 font 0" ... et ainsi de suite. B/ fonction OU (disjonction) OR allon un peu plus vite : avec l'équation : L = a+b ( à lire L = a OU b ) C / fonction NON (négation) NOT D / fonction NON ET (conjonction négative) NAND Il s'agit en fait d'une fonction ET suivie d'une fonction NON E / fonction NON OU (disjonction négative) NOR F / fonction OU EXCLUSIF ( disjonction exclusive ) XOR En général les débutants butent un peu sur celle-là... on peut la traduire ainsi : a OU b MAIS pas les deux. Voici comme d'habitude schéma, table de vérité et équation : Fun fact : les développeurs Assembleur utilisent souvent cette fonction pour remettre à 0 une variable ( un registre ) : xor ax,ax en effet, si vous vous amusez à poser l'opération ( imaginons que ax vaut 42, soit 00101010 ) : 00101010 xor 00101010 = 00000000 et oui, 0 ou 0 mais pas les deux, ça fait 0 ; 1 ou 1 MAIS PAS LES DEUX, ça fait 0... cette méthode est plus courte (en nombre d'octet) que de mettre 0 dans la variable directement : mov ax, 0 Mais on s'éloigne du sujet originel... il nous reste une dernière fonction logique ! G / fonction NON OU EXCLUSIF (disjonction exclusive négative) XNOR Il s'agit bêtement d'une xor avec une not derrière... Vous remarquez cette bulle derrière la fonction logique à la place d'un petit triangle ? c'est une autre représentation pour dire que l'on à inversé la sortie ( on y a mit une fonction NON ). Pfiou c'est fini pour la présentation bête et méchante des fonction logiques ! à noter qu'il en exister deux trois autres telles que l'implication ou l'inhibition mais bon, moins utilisées. Petit bonus : le théorème de De Morgan : première loi : deuxième loi : Vous êtes normalement capables de comprendre ceci par vous-même et j'aurais bien du mal à vous l'expliquer mieux que l'équation ! Le meilleur moyen de le maitriser est de faire des exercices... mais je n'ai pas mon cours sous la main Si ça vous intéresse : http://fr.wikipedia.org/wiki/Lois_de_De_Morgan II / faire du calcul ! aaaaaaaaah ! enfin quelque chose d'intéressant ! A / les additionneurs ( adders ) Voyons comment votre ordinateur fait des additions... (à peu près, les ingénieurs de proco on depuis longtemps abandonné cette méthode pour se tourner vers des additionneurs plus performant, notamment le Kogge-stone adder, qui est un carry-look-ahead adder (additionneur à calcul anticipé de retenue ) mais c'est pour une autre histoire ! ) commençons doucement avec le demi additionneur (half-adder) : nous allons additionner deux bits, le bit A et le bit B ( ça va pour le moment ? ) dans le cas où les deux valent 1, on aura 2 en sortie, n'est-ce pas ? il nous faudra donc prévoir deux bits de sortie pour écrire 2 en binaire : 10. Nous avons donc une sortie et une retenue, la sortie correspond à 20 et la retenue à 21 , respectivement nommées S et C (pour carry, retenue en anglais) les équations : C = A.B S = A⊕B schéma et table de vérité : Vous remarquerez que le schéma utilise des fonctions logiques que vous n'avez jamais vues... en fait c'est la représentation américaine (Wikipédia m'a lâchement lâcher (ooh un pléonasme ! ) sur ce coup), croyez-moi la fonction du dessus est une XOR et celle du dessous est une AND. faites un tour ici pour avoir les versions françaises et américaine côte à côte : http://en.wikipedia.org/wiki/Logic_gate Bien, nous pouvons maintenant additionner deux bits... mais qu'en est-il si nos nombres font plus de 1 bit chacun ? Il faudrait faire un half adder sur chaque couple de bits ( les 20 avec les 20, les 21 avec les 21 etc...) puis faire un half-adder entre la retenue des 20 et la sortie des 21 et puis.... et puis on s'écroule sur la table parce que dès qu'il y a plus de 4 bits sur chaque nombre, même le schéma sur une feuille de papier avec un crayon devient un vrai clavaire (j'ai déjà essayer en 4e...). C'est pourquoi on a inventé le full-adder ! Ce petit bijou fait la différence entre la retenue entrante et la retenue sortante, il additionne ainsi trois bits et possède deux bits en sortie. en reliant la retenue sortante (carry out) à la retenue entrante (carry in) du full-adder suivant, on additionne nos nombre sans avoir à gérer un truc ultra-compliqué. on a : A+B+Cin = S+Cout (ici le + est un "plus" et non pas un OU). Pour les équations : S = (A⊕ B )⊕Cin Cout = (A. B ) + (Cin . (A⊕ B ) ) Donc oui la fonction logique tout 0 droite est bien une OU. Je vous avais parlé de relier le Cout d'un adder au Cin du suivant... cela s'appel chainer les additionneurs, mettons que nous voulons faire A+B (plus hein, pas OU) mais que A et B font tous deux 4 bits, ils seront composé comme ceci : A3A2A1A0 et B3B2B1B0 et on chaine les adders comme suit : Et bien ma foi, nous voici rendu avec les additions ! B / la soustraction Et là, c'est le drame, vous avez peur de devoir vous replonger dans des schéma compliqués et incompréhensibles et tout reprendre de 0... Mais non ! si nous rusons il y a moyen de reprendre le travail déjà fait jusque là . Rappellez-vous ... A-B = A+(- B ). Cours de maths niveau 5e. Et pour trouver l'opposé d'un nombre binaire, c'est très simple. Cherchons -12. prenons la valeur absolue : (0b00001100), inversez-le bit à bit => 0b11110011, puis ajouter 1 => 0b11110100. Et voilà votre nombre en binaire signé ( complément à deux ) ! simple non ? et avec des fonctions logiques ? il suffit d'appliquer la fonction NON sur notre chiffre... puis de le faire passer dans un adder avec un 1. Mieux encore, regardez le schéma des full-adders chainés, n'y voyez-vous pas une première retenue entrante inutile ? le voilà notre 1 à ajouter ! pour faire une soustraction, il suffit de faire une addition, sauf que l'on met la première Cin à 1 et que l'on fait passer B par une fonction NON . Mais il y a encore mieux, on peut utiliser le même chainage d'adders pour faire des additions et des soustractions ! il suffit de faire passer B par des fonction XOR, la deuxième entrée de chaque XOR étant reliée... à Cin, ainsi si Cin est à 0, B reste inchangé, Cin est à 0 (sans blague ) et on fait une addition entre A et B. Si Cin est à 1, le XOR va inverser chaque bits de B et le chaînage d'adders va ajouter 1 en plus, on aura une soustraction entre A et B (A-B pour être précis) . en image : photoshop pro here ! Et bien voilà... vos neurones peuvent désormais reposer en paix. Si vous voulez plus de masturbation intellectuelle faites-le moi savoir et je m'attaquerai aux multiplicateurs... et si vous voulez du hardcore je vous proposerai des diviseurs... et pour l'orgasme intellectuel, il y a le sujet qui me tient le plus à coeur : les carry-look-ahead adders ( comme le kogge-stone adder dont j'avais mentionné l'existence ).